Now, I don’t know if you can run Doom on those many crabs. The sub-title to this post comes from the following tweet, which blew up on r/theydidthemath about four years ago. But hopefully, by the end of this post, you will be able to appreciate exactly why this meme is funny.
The paper that appears in the above tweet is the following: Gunji, Yukio-Pegio & Nishiyama, Yuta & Adamatzky, Andrew. (2012). Robust Soldier Crab Ball Gate. 20. 10.1063/1.3637777.
The paper itself is a fun read, but let’s try to first break down precisely what a logic gate is and how “Scientists have also successfully built logic gates using soldier crabs.”
1 + 1 = 1, and the world of boolean mathematics
Any logical statement can be assigned the label of either True or False. For instance, the statement “Fanfiction writers are the true pioneers of literary innovation” can be classified as True and 'The Death Note movie adaptations captured the essence of the manga perfectly' can be classified as False. (I will not accept any other alternative interpretations to the above statements).
Let me highlight the lack of nuance here. The statement can either be True or False; there is no in-between for a logical statement. I can construct a compound logical statement where I merge these two sentences, and it is still a logical statement with a single label for Truth.
The most common operations for combining two logical statements are AND and OR, which are the bread and butter of Boolean logic. They’re like the pizza dough and sauce of the logic world—things just fall apart without them.
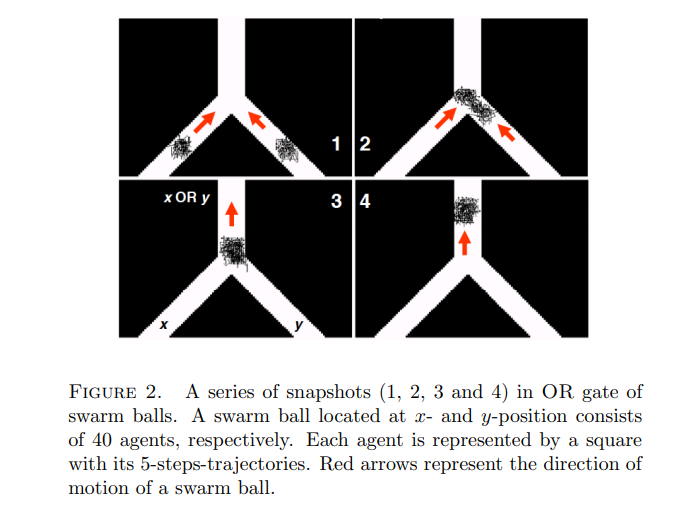
The OR operation is all about inclusion. If one of the statements in a pair is True, the entire OR statement becomes True. The OR operation only gives you a False outcome when both statements are False.
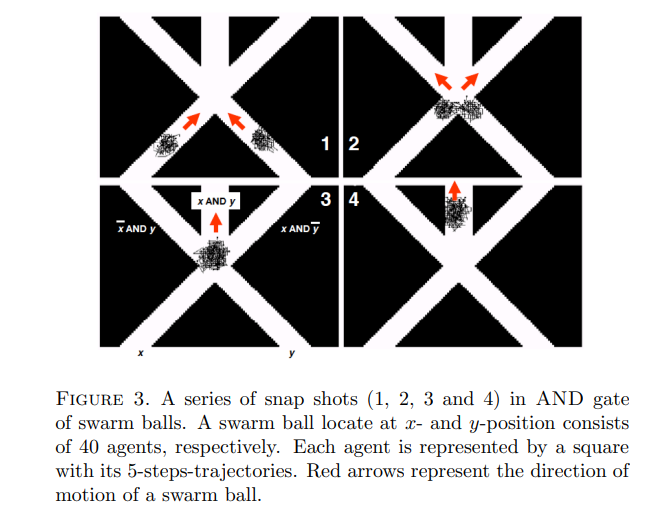
Now, the AND operation is a bit more demanding. For the AND operation to return True, both statements must be True. Even if one of the two statements are False, then the whole statement is false.
So, let’s apply this to our earlier statements:
"Fanfiction writers are the true pioneers of literary innovation" OR "The Death Note movie adaptations captured the essence of the manga perfectly."
Since at least one constituent statement is True, we can say this whole statement is True.
"Fanfiction writers are the true pioneers of literary innovation" AND "The Death Note movie adaptations captured the essence of the manga perfectly."
Now we’re dealing with an AND operator. Since at least one constituent statement is False, we can say this whole statement is False.
I can reduce this further since the sentence itself doesn’t matter; only the truth value of the sentence matters, I can just say True OR False = True, or True AND True = True. You can see how the operators both take in two inputs and spit out one output. Since I have only two possible inputs, and outputs, True or False, I can just tabulate every single possibility, which gives me what is known as a Truth table.
Since I only have two possible operations and don't want to repeatedly type "True" or "False," I'll represent "True" with 1 and "False" with 0. I'll use * for the AND operator and + for the OR operator.
Now if you’ll just refer to the truth table above for the OR operator above, you’ll see how we’ve just proved 1+1=1 in the world of Boolean Mathematics.
There’s also the negation operator, which just changes the truth value. NOT True = False, and vice-versa.
These three operators, OR, AND, and NOT together form the basis for the world of Logical Mathematics, otherwise known as Boolean Mathematics.
If I were to electronically make these operators, combining signals coming through various wires with these logical operators, I’d construct Logic Gates. And these logic gates are the basis of all our computers. At the most basic level, any computer is basically made from these logic gates arranged to perform complex operations and a few additional components to make the electronics work.
How do Crabs move around?
Now, if we want to build a logic gate with crabs, we first have to understand how the crabs move around. Perhaps with a better understanding of the way a crab moves around, we can then better make logic gates with Crabs.
The story begins when scientists observe crabs moving in the wild. The overall swarm seems to be moving in an orderly fashion, but the individual crabs move in a chaotic pattern. On top of that, we can see that the swarm has an active front and a passive tail. The tail of the swarm just follows the swarm, implying that there's some directional preference for how the individual crab will move. There's clearly some form of order within this chaos.
Let’s take a single crab and place it on the grid. There’s no rhyme or reason for which direction it’ll go, it could move around in any direction. The crab is like the king in chess; it could move to the next grid box in any of the eight directions. The possible set of positions the crab could take at the next time-step is known as the Crab’s Moore Neighbourhood.

Now let’s take three crabs and draw their Moore Neighbourhoods. Now we need to account for an additional factor. If there’s another crab already in an adjacent box, we can’t go there, so that box is out of the Moore Neighbourhood. A single box can be in the Moore Neighbourhood for multiple crabs.

We can define the popularity of the boxes in the grid, which measures how many crab’s Moore neighborhoods the box appears in. Here, the blue box would have a popularity of 3, the red boxes have a popularity of 2, the pink boxes would have a popularity of 1, and the brown boxes would have a popularity of 0.
Finally, once we're done with assigning the popularity of all the boxes, we look at the positions with the most popularity and see how many crabs can move to that position. We select one of these crabs randomly and move it to the position. We can repeat the process once we're done with the most popular sites and the crabs have moved.
The Crab-Puter
Of course, the above discussion isn't a perfect representation of how the crabs move. Each crab is an individual, and crabs don't really have an algorithmically coordinated plan on how to move when in a swarm. (Not one we properly understand, at least). There will be crabs that will wander around. It’s a process with a lot of randomness.
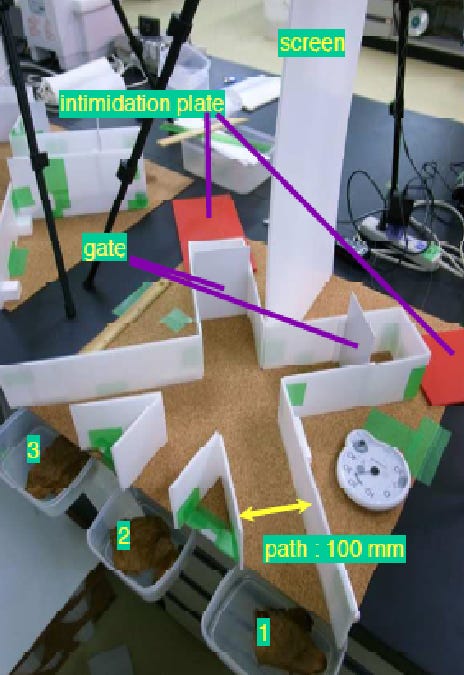
But there is one thing you can notice from the logic here. If two swarms of crabs meet at an angle, the combined swarm will move in the direction along the angle bisector of that angle. The researchers used this emergent behavior to construct the logic gates.
When you try to physically set the crabs in the following setup, because of the associated randomness, you will notice that some crabs go into the extra two roads. So, you’d have to look at how many crabs ended up on each of the roads and choose which road had the most crabs as your corresponding output. But, you CAN physically set up logic gates with crabs.
Can you actually run Doom on a Crab-Puter?
The numbers that the Redditors are commenting on seem to disagree with the Tweet, however, the number may vary with lots of considerations. If you're trying to emulate a Ti-83, like this commenter, you are getting a value of 340000 crabs to play doom. However, if you try to emulate an old PC from the time Doom originally came out, like this commenter, you get approximately 10 billion crabs, more in line with the tweet.
But as user u/obi1kenobi1 points out in a response to the first comment I linked, the biggest challenge to playing a crabby game of doom is clock speed. Each processor can do a certain number of calculations per second. The more Calculations per second, the faster the computer, the more frames you get in your Demon Slaying fun. However, for ALL the crabs to move, and in sync with each other, it would be impossible to get it to be fast enough to be meaningful in any way. To render one frame of E1M1, it'd take years, if not centuries of time in Crab Cycles.
And all this discussion is ignoring the discussion of memory, like RAM and ROM, that any computer program needs to run.
EDIT: There is something to discuss about the memory. If you can build logic gates, you can build flip-flops, which, with some necessary complexity, you can build RAM.
As fun as it might be to imagine that Doom can run even on a computer made of Crabs, it’s technically feasible, even if it’s not practically feasible.